You signed in with another tab or window. Reload to refresh your session.You signed out in another tab or window. Reload to refresh your session.You switched accounts on another tab or window. Reload to refresh your session.Dismiss alert
@@ -200,7 +200,7 @@ Now we could just leave files here, copying the entire file on write
200
200
provides the synchronization without the duplicated memory requirements
201
201
of the metadata blocks. However, we can do a bit better.
202
202
203
-
## CTZ linked-lists
203
+
## CTZ skip-lists
204
204
205
205
There are many different data structures for representing the actual
206
206
files in filesystems. Of these, the littlefs uses a rather unique [COW](https://upload.wikimedia.org/wikipedia/commons/0/0c/Cow_female_black_white.jpg)
@@ -246,26 +246,29 @@ runtime to just _read_ a file? That's awful. Keep in mind reading files are
246
246
usually the most common filesystem operation.
247
247
248
248
To avoid this problem, the littlefs uses a multilayered linked-list. For
249
-
every block that is divisible by a power of two, the block contains an
250
-
additional pointer that points back by that power of two. Another way of
251
-
thinking about this design is that there are actually many linked-lists
252
-
threaded together, with each linked-lists skipping an increasing number
253
-
of blocks. If you're familiar with data-structures, you may have also
254
-
recognized that this is a deterministic skip-list.
249
+
every nth block where n is divisible by 2^x, the block contains a pointer
250
+
to block n-2^x. So each block contains anywhere from 1 to log2(n) pointers
251
+
that skip to various sections of the preceding list. If you're familiar with
252
+
data-structures, you may have recognized that this is a type of deterministic
253
+
skip-list.
255
254
256
-
To find the power of two factors efficiently, we can use the instruction
The CTZ linked-list has quite a few interesting properties. All of the pointers
289
-
in the block can be found by just knowing the index in the list of the current
290
-
block, and, with a bit of math, the amortized overhead for the linked-list is
291
-
only two pointers per block. Most importantly, the CTZ linked-list has a
292
-
worst case lookup runtime of O(logn), which brings the runtime of reading a
293
-
file down to O(n logn). Given that the constant runtime is divided by the
294
-
amount of data we can store in a block, this is pretty reasonable.
295
-
296
-
Here is what it might look like to update a file stored with a CTZ linked-list:
291
+
We can find the runtime complexity by looking at the path to any block from
292
+
the block containing the most pointers. Every step along the path divides
293
+
the search space for the block in half. This gives us a runtime of O(log n).
294
+
To get to the block with the most pointers, we can perform the same steps
295
+
backwards, which keeps the asymptotic runtime at O(log n). The interesting
296
+
part about this data structure is that this optimal path occurs naturally
297
+
if we greedily choose the pointer that covers the most distance without passing
298
+
our target block.
299
+
300
+
So now we have a representation of files that can be appended trivially with
301
+
a runtime of O(1), and can be read with a worst case runtime of O(n logn).
302
+
Given that the the runtime is also divided by the amount of data we can store
303
+
in a block, this is pretty reasonable.
304
+
305
+
Unfortunately, the CTZ skip-list comes with a few questions that aren't
306
+
straightforward to answer. What is the overhead? How do we handle more
307
+
pointers than we can store in a block?
308
+
309
+
One way to find the overhead per block is to look at the data structure as
310
+
multiple layers of linked-lists. Each linked-list skips twice as many blocks
311
+
as the previous linked-list. Or another way of looking at it is that each
312
+
linked-list uses half as much storage per block as the previous linked-list.
313
+
As we approach infinity, the number of pointers per block forms a geometric
314
+
series. Solving this geometric series gives us an average of only 2 pointers
315
+
per block.
316
+
317
+
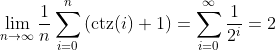
318
+
319
+
Finding the maximum number of pointers in a block is a bit more complicated,
320
+
but since our file size is limited by the integer width we use to store the
321
+
size, we can solve for it. Setting the overhead of the maximum pointers equal
322
+
to the block size we get the following equation. Note that a smaller block size
323
+
results in more pointers, and a larger word width results in larger pointers.
0 commit comments