🧠 Transformer-from-Scratch (PyTorch)

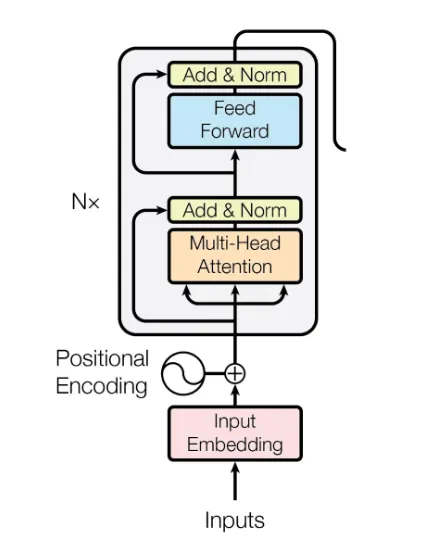
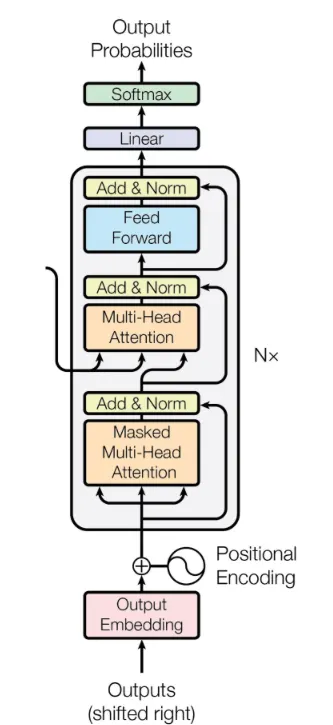
A complete implementation of the Transformer architecture from scratch using PyTorch. This project aims to help researchers, students, and enthusiasts understand the inner workings of the Transformer model without relying on high-level abstractions from libraries like HuggingFace or Fairseq.

📌 Features

• Custom implementation of:

  • Positional Encoding
  • Scaled Dot-Product Attention
  • Multi-Head Attention
  • Feedforward Network
  • Encoder & Decoder Stacks
  • Attention Masking

• Easy to read and modular code

• Designed for educational clarity and flexibility

🔹 Understanding Self-Attention in Multi-Head Attention

Step 1: Tokenization and Embedding

Before attention is applied, each word in the sentence is tokenized, then converted into embeddings, concatenated with its positional encoding, and finally represented as a numerical vector (embedding).

• In the "Attention Is All You Need" paper, d_model = 512. Each word is represented as a 1D vector of 512 dimensions (512D).

Example Sentence:

"Hi how are you"

Each word is converted into a vector:

• "Hi" → [0.1, 0.3, 0.7, ...] (Size: d_model)
• "how" → [0.2, 0.6, 0.5, ...] (Size: d_model)
• "are" → [0.4, 0.2, 0.8, ...] (Size: d_model)
• "you" → [0.9, 0.1, 0.3, ...] (Size: d_model)

At this point, each word is just an embedding vector of size d_model.

Note: Positional encoding is added to each embedding to retain word order information.

---

Step 2: Creating Query (Q), Key (K), and Value (V)

For each word, we create three separate vectors:

• Query (Q) → Determines how much focus a word should get.
• Key (K) → Helps decide how much attention a word receives from other words.
• Value (V) → Contains the actual word information to be passed on.

These vectors are computed using linear transformations:

Q = W_q * X

K = W_k * X

V = W_v * X

where ( W_q, W_k, W_v ) are learnable weight matrices. Whereas, X represents the input embeddings of the words/tokens in the sentence.

For example, for the word "Hi", we get:

• Query vector Q_hi (size: d_model = 512D)
• Key vector K_hi (size: d_model = 512D)
• Value vector V_hi (size: d_model = 512D)

This same process applies to all other words.

---

Step 3: Compute Attention Scores in One Head

Now, we compare how much each word should attend to every other word in the sentence. This is done by computing the dot product between the query of one word and the keys of all words.

Since multi-head attention is used, each head works with a smaller subspace:

• d_k = d_model / num_heads
• If d_model = 512 and num_heads = 8, then d_k = 512 / 8 = 64.
• Each head gets Q, K, V vectors of size 64D.

Word	Query (Q)	Key (K)	Value (V)
Hi	Q_hi (64D)	K_hi (64D)	V_hi (64D)
How	Q_how (64D)	K_how (64D)	V_how (64D)
Are	Q_are (64D)	K_are (64D)	V_are (64D)
You	Q_you (64D)	K_you (64D)	V_you (64D)

Step 3.1: Compute Raw Scores

For word Hi, we compute the dot product of its query with the keys of all words:

Score1= Q_hi.K_hi

Score2= Q_hi.K_how

Score3= Q_hi.K_are

Score4= Q_hi.K_you

Step 3.2: Apply Softmax

The scores are scaled to avoid large gradients by dividing by ( \sqrt{d_k} ) and then passed through softmax to get probabilities:

$$ \text{Attention Weight} = \text{softmax} \left( \frac{Q \cdot K^T}{\sqrt{d_k}} \right) $$

$$ \text{Attention Weight}_i = \text{softmax} \left(Score_i\right) $$

Each word now has an attention score that tells how much focus it should give to the other words.

Step 3.3: Compute Final Weighted Sum

Multiply each attention weight by the corresponding Value (V) vector:

Output1= Weight1*V_hi

Output2= Weight2*V_how

Output3= Weight2*V_are

Output4= Weight4*V_you

Final embedding for the word Hi is: Output1 + Output2 + Output3 + Output4

Each output is 64D, so we get one 64D vector per word per attention head.

Note: We have Calculated Final Contexual Embeddings of word Hi. Similarly, we have to for other words how, are, you. This is done by computing the dot product between the query of one word and the keys of all words.

---

Step 4: Multi-Head Attention

Since we have 8 heads, each computes separate self-attention and gives an output of size (batch, seq_length, d_k) = (1, 4, 64).

🔹Understanding FeedForward In Transformer

The Position-Wise Feed Forward Network (FFN) is a key component of the Transformer architecture. It is applied independently to each token in the sequence after multi-head attention.

• Multi-head attention captures relationships between words, but it does not change individual word representations much.
• The FFN introduces non-linearity and richer transformations to enhance each token’s representation.
• It consists of two linear transformations with a ReLU activation in between.

🔹 Positional Encoding

How Positional Encoding Works?

Since self-attention treats all words independently, it doesn't understand their order. Positional encoding assigns each position a unique vector, ensuring the model understands word order.

Step 1: Convert Words to Word Embeddings

Before adding positional encoding, each word gets converted into a 512-dimensional vector using an embedding layer.

Let's assume our embedding model has an embedding size (d_model) of 512.

Token	Word Embedding (Simplified: 3D instead of 512D)
Hi	[0.3, 0.5, -0.2]
How	[0.7, -0.1, 0.9]
Are	[-0.5, 0.3, 0.6]
You	[0.1, -0.4, 0.8]

---

Step 2: Generate Unique Positional Encoding

Each position (0, 1, 2, 3) is assigned a unique vector using a combination of sine and cosine functions at different frequencies.

Formula:

Each position p (word index) is assigned a 512-dimensional vector using:

$$ PE(p, 2i) = \sin\left(\frac{p}{10000^{\frac{2i}{d_{\text{model}}}}}\right) $$

$$ PE(p, 2i+1) = \cos\left(\frac{p}{10000^{\frac{2i}{d_{\text{model}}}}}\right) $$

where:

• p = Position index (0 for "Hi", 1 for "How", etc.)
• i = Dimension index (half use sin, half use cos)
• d_model = Embedding size (e.g., 512)
• 10000 = A constant to control frequency scaling

For simplicity, let's assume d_model = 6 instead of 512:

Position p	PE(0) (sin)	PE(1) (cos)	PE(2) (sin)	PE(3) (cos)	PE(4) (sin)	PE(5) (cos)
0 (Hi)	0.0000	1.0000	0.0000	1.0000	0.0000	1.0000
1 (How)	0.8415	0.5403	0.4207	0.9070	0.2104	0.9775
2 (Are)	0.9093	-0.4161	0.6543	0.7561	0.3784	0.9256
3 (You)	0.1411	-0.9900	0.8415	0.5403	0.5000	0.8660

Each position receives a unique vector, ensuring that different words have different encodings.

---

Step 3: Add Positional Encoding to Word Embeddings

Each word’s embedding is element-wise added to its corresponding positional encoding.

Token	Word Embedding	Positional Encoding	Final Embedding (Word + PE)
Hi	[0.3, 0.5, -0.2]	[0.00, 1.00, 0.00]	[0.3, 1.5, -0.2]
How	[0.7, -0.1, 0.9]	[0.84, 0.54, 0.42]	[1.54, 0.44, 1.32]
Are	[-0.5, 0.3, 0.6]	[0.91, -0.41, 0.65]	[0.41, -0.11, 1.25]
You	[0.1, -0.4, 0.8]	[0.14, -0.99, 0.84]	[0.24, -1.39, 1.64]

---

🔹 Encoder Block

🔹 Decoder Block

🔹 Understanding Masked Self-Attention in Multi-Head Attention

1. Translation and Tokens

• English: “Hi how are you” [this we pass from encoder block]
• Hindi: “हाय कैसे हो तुम” [ this we pass in decoder block while training so it is non autogressive in training]

Token sequence (4 tokens):

["हाय", "कैसे", "हो", "तुम"]

---

2. Q, K, V Matrices

We stack each token’s Q/K/V vectors into 4×4 matrices (rows = tokens, cols = d_model = 4):
(In the original Attention paper, we have d_model = 512)

Q Matrix:

$$ Q = \begin{bmatrix} 0.1 & 0.2 & 0.3 & 0.4 \\\ 0.2 & 0.1 & 0.4 & 0.3 \\\ 0.3 & 0.4 & 0.2 & 0.1 \\\ 0.4 & 0.3 & 0.1 & 0.2 \end{bmatrix} $$

K Matrix:

$$ K = \begin{bmatrix} 0.4 & 0.3 & 0.2 & 0.1 \\\ 0.5 & 0.3 & 0.6 & 0.1 \\\ 0.6 & 0.4 & 0.5 & 0.2 \\\ 0.1 & 0.2 & 0.3 & 0.5 \end{bmatrix} $$

V Matrix:

$$ V = \begin{bmatrix} 0.1 & 0.5 & 0.2 & 0.4 \\\ 0.3 & 0.7 & 0.4 & 0.1 \\\ 0.2 & 0.3 & 0.5 & 0.3 \\\ 0.6 & 0.4 & 0.3 & 0.2 \end{bmatrix} $$

Token-wise mapping:

• 1st row of Q, K, V → हाय
• 2nd row of Q, K, V → कैसे
• 3rd row of Q, K, V → हो
• 4th row of Q, K, V → तुम

3. Raw Attention Scores

We compute the raw attention scores using:

$$ S = \left( \frac{Q \cdot K^T}{\sqrt{d_k}} \right) $$

Each row i contains the dot products of token i’s Q vector with every token’s K vector:

Raw Attention Score Matrix:

$$ S = \begin{bmatrix} 0.20 & 0.33 & 0.37 & 0.34 \\\ 0.22 & 0.40 & 0.42 & 0.31 \\\ 0.29 & 0.40 & 0.46 & 0.22 \\\ 0.29 & 0.37 & 0.45 & 0.23 \end{bmatrix} $$

Row-to-token mapping:

• 1st row → हाय
• 2nd row → कैसे
• 3rd row → हो
• 4th row → तुम

4. Causal Mask

We enforce autoregressive order by masking out future positions.
(At हाय, we don’t know the rest of the words, so we mask them with $-\infty$ since $\text{softmax}(-\infty) = 0$. Same for all other tokens.)

Mask Matrix:

$$ \text{Mask} = \begin{bmatrix} 0 & -\infty & -\infty & -\infty \\ % हाय (i=0) 0 & 0 & -\infty & -\infty \\ % कैसे (i=1) 0 & 0 & 0 & -\infty \\ % हो (i=2) 0 & 0 & 0 & 0 % तुम (i=3) \end{bmatrix} $$

We then add this mask to the raw score matrix S to get the masked scores S′:

Masked Score Matrix:

$$ S' = S + \text{Mask} = \begin{bmatrix} 0.20 & -\infty & -\infty & -\infty \\\ 0.22 & 0.40 & -\infty & -\infty \\\ 0.29 & 0.40 & 0.46 & -\infty \\\ 0.29 & 0.37 & 0.45 & 0.23 \end{bmatrix} $$

5. Softmax → Attention Weights

We apply softmax row-wise to the masked score matrix (ignoring $-\infty$ entries, which effectively become 0 after softmax):

Softmax Weight Matrix:

$$ W = \begin{bmatrix} 1.000 & 0 & 0 & 0 \\[6pt] 0.455 & 0.545 & 0 & 0 \\[6pt] 0.303 & 0.338 & 0.359 & 0 \\[6pt] 0.238 & 0.258 & 0.280 & 0.224 \end{bmatrix} $$

Interpretation by token:

• Row “हाय” → attends only to itself: [1, 0, 0, 0]
• Row “कैसे” → softmax((0.22, 0.40) \approx (0.455, 0.545))
• Row “हो” → softmax((0.29, 0.40, 0.46) \approx (0.303, 0.338, 0.359))
• Row “तुम” → softmax((0.29, 0.37, 0.45, 0.23) \approx (0.238, 0.258, 0.280, 0.224))

6. Final Output

We compute the contextualized output vectors by multiplying the attention weights W with the Value matrix V:

$$ O = W \times V = \begin{bmatrix} 1 \cdot V_{\text{हाय}} \ 0.455 \cdot V_{\text{हाय}} + 0.545 \cdot V_{\text{कैसे}} \ 0.303 \cdot V_{\text{हाय}} + 0.338 \cdot V_{\text{कैसे}} + 0.359 \cdot V_{\text{हो}} \ 0.238 \cdot V_{\text{हाय}} + 0.258 \cdot V_{\text{कैसे}} + 0.280 \cdot V_{\text{हो}} + 0.224 \cdot V_{\text{तुम}} \end{bmatrix}

\begin{bmatrix} 0.10 & 0.50 & 0.20 & 0.40 \ 0.209 & 0.609 & 0.309 & 0.237 \ 0.2035 & 0.4958 & 0.3753 & 0.2627 \ 0.2916 & 0.4732 & 0.3580 & 0.2498 \end{bmatrix} $$

Interpretation by token:

• Output “हाय” → [0.10, 0.50, 0.20, 0.40]
• Output “कैसे” → ≈ [0.209, 0.609, 0.309, 0.237]
• Output “हो” → ≈ [0.2035, 0.4958, 0.3753, 0.2627]
• Output “तुम” → ≈ [0.2916, 0.4732, 0.3580, 0.2498]

🔹 Understanding Cross‑Attention in Encoder–Decoder Attention

Below is a step‑by‑step worked example of cross‑attention between an English source (“Hi how are you”) and its Hindi translation (“हाय कैसे हो तुम”), using toy matrices (with model dimension d_model = 4(In Attention paper we have 512D vector)).

1. Source & Target Tokens

• Encoder (English):
  “Hi how are you”
  → Tokens:

  ["Hi", "how", "are", "you"]
  

• Decoder (Hindi):
  “हाय कैसे हो तुम”
  → Tokens (feeding in at one time during training):

  ["हाय", "कैसे", "हो", "तुम"]
  

2. Q, K, V Matrices

• Queries come from the decoder hidden states (one per Hindi token):

$$ Q = \begin{bmatrix} 0.1 & 0.2 & 0.3 & 0.4 \\\ 0.2 & 0.1 & 0.4 & 0.3 \\\ 0.3 & 0.4 & 0.2 & 0.1 \\\ 0.4 & 0.3 & 0.1 & 0.2 \end{bmatrix} $$

Rows represent Hindi tokens:

• Row 1 → हाय

• Row 2 → कैसे

• Row 3 → हो

• Row 4 → तुम

• Keys and Values come from the encoder outputs (one per English token):

$$ K = \begin{bmatrix} 0.4 & 0.3 & 0.2 & 0.1 \\\ 0.5 & 0.3 & 0.6 & 0.1 \\\ 0.6 & 0.4 & 0.5 & 0.2 \\\ 0.1 & 0.2 & 0.3 & 0.5 \end{bmatrix}, \quad V = \begin{bmatrix} 0.1 & 0.5 & 0.2 & 0.4 \\\ 0.3 & 0.7 & 0.4 & 0.1 \\\ 0.2 & 0.3 & 0.5 & 0.3 \\\ 0.6 & 0.4 & 0.3 & 0.2 \end{bmatrix} $$

Rows represent English tokens:

• Row 1 → “Hi”
• Row 2 → “how”
• Row 3 → “are”
• Row 4 → “you”

3. Raw Cross‑Attention Scores

Compute: $$ S = \left( \frac{Q \cdot K^T}{\sqrt{d_k}} \right) $$

The raw attention score matrix:

$$ S = \begin{bmatrix} 0.20 & 0.33 & 0.37 & 0.34 \\\ 0.22 & 0.40 & 0.42 & 0.31 \\\ 0.29 & 0.40 & 0.46 & 0.22 \\\ 0.29 & 0.37 & 0.45 & 0.23 \end{bmatrix} $$

Token-wise attention scores:

• Row 1 (“हाय”) → [0.20, 0.33, 0.37, 0.34]
• Row 2 (“कैसे”) → [0.22, 0.40, 0.42, 0.31]
• Row 3 (“हो”) → [0.29, 0.40, 0.46, 0.22]
• Row 4 (“तुम”) → [0.29, 0.37, 0.45, 0.23]

Here's the corrected and properly formatted Markdown version of your content that works well with platforms supporting LaTeX math (like Jupyter Notebook or some Markdown parsers that use MathJax or KaTeX):

---

4. Softmax → Attention Weights

$$ \text{Attention Weight}(W) = \text{softmax} \left( \frac{Q \cdot K^T}{\sqrt{d_k}} \right) $$

$$ \text{Attention Weight}_i(W) = \text{softmax}(Score_i) $$

$$ \begin{bmatrix} 0.223 & 0.254 & 0.265 & 0.259 \[4pt] 0.222 & 0.265 & 0.271 & 0.242 \[4pt] 0.236 & 0.264 & 0.279 & 0.221 \[4pt] 0.238 & 0.258 & 0.280 & 0.224 \end{bmatrix} $$

• Row “हाय”: attends most to “are” (0.265) and “you” (0.259)
• Row “तुम”: attends most to “are” (0.280)

---

5. Contextualized Outputs (with explicit weighted sums)

$$ W = \begin{bmatrix} 0.223 & 0.254 & 0.265 & 0.259 \[4pt] 0.222 & 0.265 & 0.271 & 0.242 \[4pt] 0.236 & 0.264 & 0.279 & 0.221 \[4pt] 0.238 & 0.258 & 0.280 & 0.224 \end{bmatrix} \quad V = \begin{bmatrix} V_{\text{Hi}} = [0.1,,0.5,,0.2,,0.4] \[3pt] V_{\text{how}} = [0.3,,0.7,,0.4,,0.1] \[3pt] V_{\text{are}} = [0.2,,0.3,,0.5,,0.3] \[3pt] V_{\text{you}} = [0.6,,0.4,,0.3,,0.2] \end{bmatrix} $$

Each output row is a weighted sum of the encoder values:

1. “हाय”

$$ \begin{aligned} O_{\text{हाय}} &= 0.223,V_{\text{Hi}} + 0.254,V_{\text{how}} + 0.265,V_{\text{are}} + 0.259,V_{\text{you}} \\ &\approx [0.307,,0.472,,0.356,,0.246] \end{aligned} $$

2. “कैसे”

$$ \begin{aligned} O_{\text{कैसे}} &= 0.222,V_{\text{Hi}} + 0.265,V_{\text{how}} + 0.271,V_{\text{are}} + 0.242,V_{\text{you}} \\ &\approx [0.301,,0.475,,0.359,,0.245] \end{aligned} $$

3. “हो”

$$ \begin{aligned} O_{\text{हो}} &= 0.236,V_{\text{Hi}} + 0.264,V_{\text{how}} + 0.279,V_{\text{are}} + 0.221,V_{\text{you}} \\ &\approx [0.291,,0.475,,0.359,,0.249] \end{aligned} $$

4. “तुम”

$$ \begin{aligned} O_{\text{तुम}} &= 0.238,V_{\text{Hi}} + 0.258,V_{\text{how}} + 0.280,V_{\text{are}} + 0.224,V_{\text{you}} \\ &\approx [0.292,,0.473,,0.358,,0.250] \end{aligned} $$

$$ O = \begin{bmatrix} 0.307 & 0.472 & 0.356 & 0.246 \[4pt] 0.301 & 0.475 & 0.359 & 0.245 \[4pt] 0.291 & 0.475 & 0.359 & 0.249 \[4pt] 0.292 & 0.473 & 0.358 & 0.250 \end{bmatrix} $$

• Row 1 (“हाय”)
• Row 2 (“कैसे”)
• Row 3 (“हो”)
• Row 4 (“तुम”)