Add Tutorial for LOJ-1266: Points in Rectangle (en)

1266/en.md

@@ -0,0 +1,119 @@
+# LightOj 1266 - Points in Rectangle
+[Problem Statement](http://lightoj.com/volume_showproblem.php?problem=1266)  
+### Summary
+You will be given two type of query and the range of query is 1<=q<=3000. Two type of query is -
+1. 0 x y  that means add a point in (x,y) co-ordinate if it doesn't already exist.
+2. 1 x1 y1 x2 y2 - you have to find the number of point exist in this range where     (x1,y1) is lower left corner of rectangle and (x2,y2) is upper right corner.
+
+### Tag
+Data Structure , Binary index tree
+### Quick links for prerequisites
+Binray index tree:  
+https://www.geeksforgeeks.org/binary-indexed-tree-or-fenwick-tree-2
+https://cp-algorithms.com/data_structures/fenwick.html
+### Observation 
+In basic BIT (binary index tree) we deal with one dimentional array . The difference is here we have to deal with both X and Y value. so if we take two dimentional array for saving segmented sum . Here BIT[X][Y] denotes for each x index we have another array for Y value. 
+### Solution 
+1. for first type of query we will just update the point in (x,y) index with value 1 which mainly represent number of point in that index. As it is told only one point exist in one point so value used for update always 1. But if that point is already updated then we don't have to update it.
+2. The come to second type of query . Here two index is given . Now how to use our query function?? lets look at the image bellow-
+![first](https://user-images.githubusercontent.com/52863153/227806473-b97210cb-ed3d-4978-962a-b1d02bff6eb0.png)
+
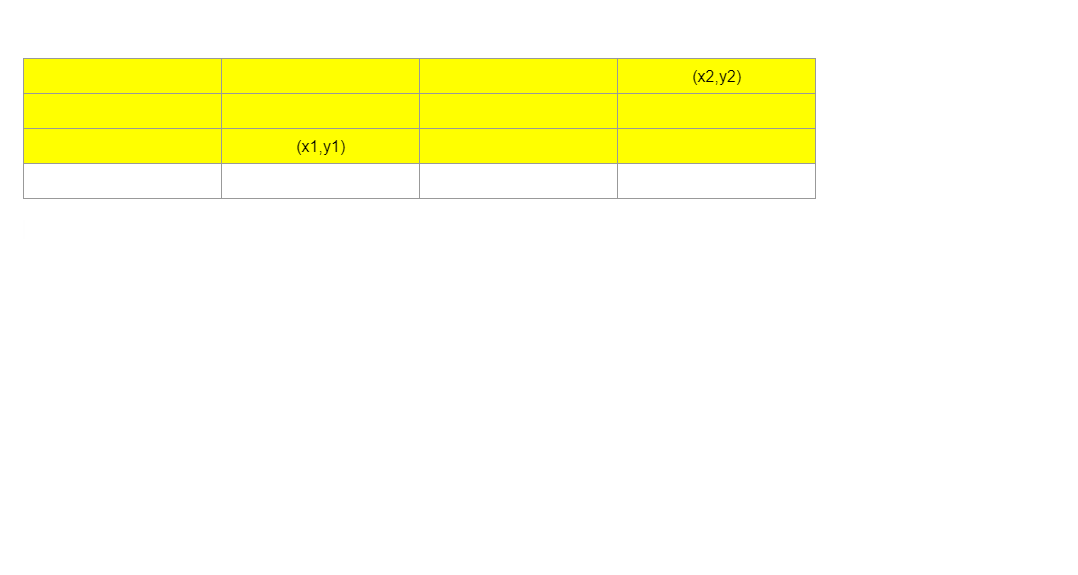
+from above image we have to find number of point in green colored rectangle. <br>
+so firstly query(x2,y2)-query(x2,y1-1) denotes the rectengle bellow with colored yellow shown bellow
+
+![second](https://user-images.githubusercontent.com/52863153/227806592-5822527d-32a8-4300-ab63-989753d6a8d0.png)
+but we have to avoid the left part which is marked in image bellow with colored red.
+![third](https://user-images.githubusercontent.com/52863153/227806619-5faad985-a9d9-4aec-ba8e-7ddb624d2570.png)
+so final ans <br>
+=query(x2,y2)-query(x2,y1-1)-{ query(x1-1,y2)-query(x1-1,y1-1)} <br>
+=query(x2,y2)-query(x2,y1-1)-query(x1-1,y2)+query(x1-1,y1-1) <br>
+then we can find easily number of point from BIT array 
+
+### Code
+
+#### C++
+```cpp
+#include<bits/stdc++.h>
+using namespace std;
+#define ll  long long int
+const ll N=2e6+5;
+const ll mod=1000000007;
+ll BIT[1005][1005];
+bool vis[1005][1005];
+void update(int x, int y , int val)
+{
+    while(x<=1001)
+    {
+        int y1=y;
+        while(y1<=1001)
+        {
+            BIT[x][y1]+=val;
+            y1+=(y1&-y1);
+        }
+        x+=(x&-x);
+    }
+}
+ll query(int x, int y)
+{
+    ll sum=0;
+    while(x>0)
+    {
+        int y1=y;
+        while(y1>0)
+        {
+            sum+=BIT[x][y1];
+            y1-=(y1&-y1);
+        }
+        x-=(x&-x);
+    }
+    return sum;
+}
+void solve()
+{
+
+   memset(BIT,0,sizeof(BIT)); //initialize with zero 
+   memset(vis,false,sizeof(vis)); // initalize with zero
+   ll q,a,b,c,d,x1,y1,x2,y2;
+   cin>>q;
+   while(q--)
+   {
+      cin>>a;
+      if(a==0)
+      {
+         cin>>a>>b;
+         a++,b++;
+         if(!vis[a][b])
+         {
+            vis[a][b]=true; 
+            update(a,b,1); //update the index 
+         }
+      }
+      else
+      {
+         cin>>x1>>y1>>x2>>y2;
+         x1++,x2++,y1++,y2++;
+         ll ans=query(x2,y2)-query(x2,y1-1)-query(x1-1,y2)+query(x1-1,y1-1); /* find total point inside the given rectengle */
+         cout<<ans<<endl;
+      }
+   }
+
+
+   return;
+}
+int32_t main()
+{
+
+
+
+  int tt;
+  tt = 1;
+  cin>>tt;
+  for(int i=1;i<=tt;i++)
+  {
+     cout<<"Case "<<i<<":"<<endl;
+     solve();
+  }
+  return 0;
+}
+```
+##### Happy_coding (inshallah! One day you will be rewarded for your hardwork )